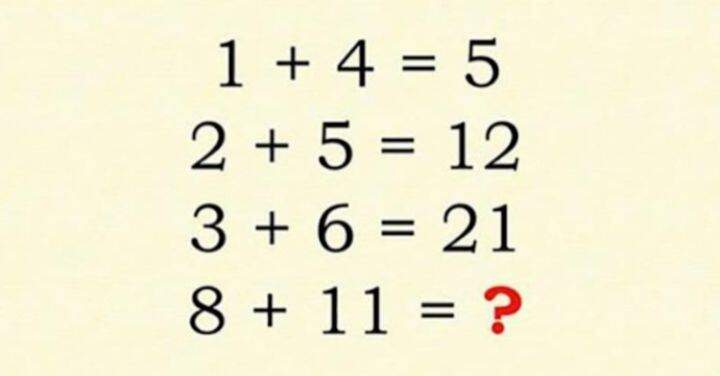
這道題最早出現在《每日郵報》上,由Go Tumble在Wikr上出的題目。這道題有2個答案:40 和 96
-
第一個答案的解題思路:後一個等式的和+前一個等式的和。
-
第一行:1 + 4 = 5
-
第二行:2 + 5 = 7,而題目中的和是12,因此可得5 + 7 = 12
-
第三行:3 + 6= 9,而題目中的和是21,因此可得 9 + 12 = 21
-
以此類推:8 + 11 = 19,因此最終答案是19 + 21 = 40
-
第二種解題思路:將等式中的第二個數拆解成2數相乘,使得等式兩邊結果成立。
-
第一行:1 + (4 x 1) = 5
-
第二行:2 + (5 x 2) = 12
-
第三方:3 + (6 x 3) = 21
-
以此類推:8 + (11 x 8) = 96
-
-
、
-
-
-
-
-
-
-
-
-
-
-
--
-
-
-
-
-
-
-
-
有趣的數學題:

第一題要求學生使用重復加法表示5×3,學生的答案是5+5+5=15,老師批錯,正確答案是 3 + 3 + 3 + 3 + 3 = 15
第二題要求學生用數組表示4×6,學生畫出一個6行4列的矩陣來表示,老師批錯,正確答案是一個6列4行的矩陣。
這樣的試題引起了大家的極大反響,有人認為這樣死板的答案會影響到學生以後對乘法交換的理解,因為根據乘法交換律4×6=6×4,而這樣的答案是在告訴學生,規律並不正確。

新加坡的一位主持人首次將這道小學5年級的邏輯題發布到Facebook上,被轉發了近6000次。這道題的問題是Cheryl的生日是哪一天?題中,Cheryl告訴 Albert和Bernard不同的線索,一人只知道日期,另一人只知道月份,根據2人的對話最後找出Cheryl的生日。最終的答案是7月16日。之後被發現這道題並不是新加坡普通小學生做的題目,而是新加坡和亞洲學校數學奧林匹克比賽(SASMO)中的一道奧數題。
《紐約時報》為此專門發布了解題思路:這種題目挑戰的是人類的思維方式。在此題中有個前提是每個人說的都是真話,因此可以根據每個人所說的話進行判斷。經常做奧數題的學生對此非常熟悉,而大部分普通人如果不經過長期的思維訓練看完題目也是一臉懵逼。
要解這道題需要將題中出現的10個日期畫成一張表格:

接著開始分析Albert和Bernard說的話,首先是Albert:
我不知道Cheryl的生日,Bernard也不知道。
從前半句可以得出Albert只知道月份,不知道日期。重點在後半句話!Bernard什麼情況下會知道生日?假設他只知道日期,如果Cheryl告訴他是19日,那麼生日只能是5月19日,如果告訴他是18日,那麼生日只能是6月18日。
因此從Albert的陳述中可以得出,Cheryl的生日月份不是5月或6月。
所以Bernard的回答是:
一開始我不知道,現在我知道了。
從Albert的陳述中,Bernard也知道了Cheryl的生日不在5月或6月,剩下的可能是7月14日、7月16日、8月14日、8月15日、8月17日。現在假設Bernard知道了生日的具體日期,如果Cheryl告訴他的是14日,Bernard還是不能確定生日,因為有2中可能性,7月14日和8月14日,因此可以排除14日。最後剩下3種可能:7月16日,8月15日,8月17日。由於Bernard知道日期,因此知道了Cheryl生日是7月16日。
所以Albert接著說
現在我也知道Cheryl的生日了。
假設Albert只知道月份,從Bernard的話中就可以確定Cheryl的生日是7月16日,因為如果是8月,那麼Bernard還是無法確定到底是8月15日還是8月17日。現在Bernard已經確定了生日,可知只能是7月16日。